Difference between revisions of "Krupakar Dhinakaran"
From Hackteria Wiki
| Line 17: | Line 17: | ||
As an introduction to all our efforts: | As an introduction to all our efforts: | ||
| − | [[http://web.mit.edu/newsoffice/2009/diy-bio-0113.html]] | + | Mit and what we are doing[[http://web.mit.edu/newsoffice/2009/diy-bio-0113.html]] |
Something done: | Something done: | ||
| − | [[http://technocrat.net/d/2008/2/7/35802/]] | + | Bactoblood[[http://technocrat.net/d/2008/2/7/35802/]] |
I am beginning to think about electricity conducting bacteria. | I am beginning to think about electricity conducting bacteria. | ||
Revision as of 09:22, 16 May 2009
Name: Krupakar Dhinakaran
Institution: Srishti, Bangalore
15th May 09
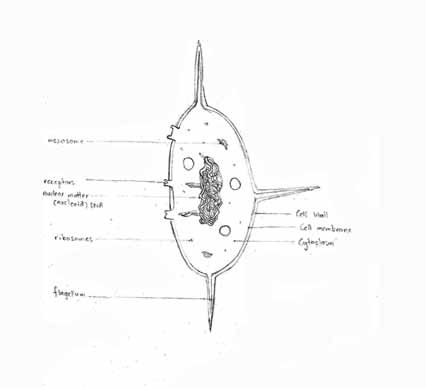
We created conceptual bacteria models.
The first diagram is the immuno-bacteria. Following it is the way it is used to clean water that has water borne-diseases and produce drinkable water.
16th May 09
As an introduction to all our efforts: Mit and what we are doing[[1]]
Something done: Bactoblood[[2]]
I am beginning to think about electricity conducting bacteria.